6. The Displacement Four Vector

In this chapter, we will take a deep dive into the properties of the displacement four vector, using all the tools developed in the previous chapters. Some of the material will repeat what has been presented already, but in more depth.

6.1. The Difference Between Two Events

The model we will be using to predict the behavior of systems moving with speeds significant compared to the speed of light require that the physical process be one such that there are two events occurring that can be viewed by different observers. Some examples of physical processes that can be understood this way are:

1. A strange particle being produced (first event), and at some later time, decaying into other particles (second event).

2. A rocket ship leaving the earth (first event), and arriving at another star (second event).

3. A high energy electron striking a proton (first event) and then being scattered and leaving the interaction area at a different energy and direction of motion from the initial electron (second event).

4. A photon with energy in the radar range sent out by a cop (first event) that is reflected by a moving car, and then returns to the cop at a different energy (second event)

5. A star cruiser traveling at 0.900 the speed of light (first event) and then shooting of a laser pulse at an angle of \(30^\circ\) with respect to the direction of motion of the star cruiser (second event).

6. A high energy proton entering the magnetic field of a bubble chamber (first event) and this same proton leaving the magnetic field traveling in a different direction (second event).

This model (which of course is special relativity) suggests how an inertial observer, such as one that is moving at a constant speed (not accelerating), should analyze what is different about the two events. It also provides a way (called the Lorentz transformation) of calculating what other inertial observers, moving with respect to the first observer, would measure as the difference between these two events.

6.2. A Summary of The Story So Far

Before diving into the analysis, a quick summary of what we have established so far. Fig. 6.1 reproduces Fig. 4.1, showing two events in spacetime diagram with a displacement four vector between them.

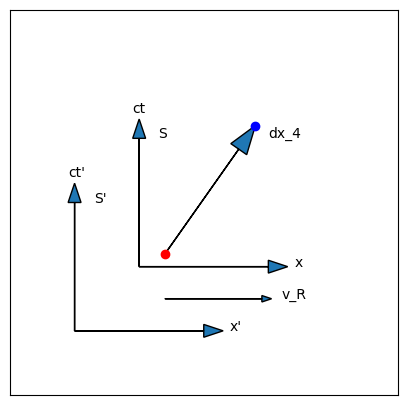
Fig. 6.1 Two events in a spacetime diagram with a displacement four vector between them.

The displacement between these two events is to be analyzed by two inertial observers traveling at a relative velocity of \(\beta_R\) with respect to each other. By convention, the \(x\)-axis is chosen such that the relative velocity points in the \(+x\) direction. Each of the observers measures the physical displacement \((dx,dy,dz)\) and the time interval \((dt)\) between the two events. Using the measured values, each observer then constructs the displacement 4-vector that describes these two events:

(6.1)\[\begin{split}[dx_4] = \begin{bmatrix} icdt\\ dx\\ dy\\ dz \end{bmatrix} \hspace{1cm} [dx_4]' = \begin{bmatrix} icdt'\\ dx'\\ dy'\\ dz' \end{bmatrix}\end{split}\]

Now, as an example, let us consider the displacement 4-vector as measured by two different observers. For simplicitly, we assume the two events as measured by the unprimed observer (shown in Fig. 6.1) have real displacements \(dy\) and \(dz\) equal O. We can therefore ignore the last two components and write the displacement 4-vector in the unprimed coordinate system as:

(6.2)\[\begin{split}[dx_4] = \begin{bmatrix} icdt\\ dx \end{bmatrix}\end{split}\]

The elements of the displacement 4-vector as measured by the primed observer are found by operating on the unprimed displacement 4-vector (equation (6.2)) with the Lorentz transformation (equation (4.7)) for relative velocity of \(\beta_R\) in the \(+x\) direction.

\[[dx_4]^\prime = {\cal L}_x(\beta_R) [dx_4]\]

(6.3)\[\begin{split}\begin{bmatrix} icdt^\prime\\ dx' \end{bmatrix} = \begin{bmatrix} \gamma_R & -i\beta_R\gamma_R\\ i\beta_R\gamma_R & \gamma_R \end{bmatrix} \begin{bmatrix} icdt\\ dx \end{bmatrix}\end{split}\]

Why didn’t Newton notice this?

In Newton’s time,a relative velocity of \(1 \times 10^4\) m/s (the orbital speed of the moon) was about as large as a relative velocity he could see. This implies \(\beta_R = 3.3 \times 10^{-5}\) and \(\gamma_R = (1 + 5\times10^{-11})\). The value for \(\gamma_R\) is really very close to 1, so it is not surprising that Newton missed this small effect! The time interval in any frame would have been less than a trillionth of a fractional change away from any other frame. It’s no wonder Newton assumed time intervals were the same in any frame!

Multiplying out the matrix equation (6.3) to find the components of the displacement 4-vector as measured by the primed observer in terms of the values of the components measured by the unprimed observer gives:

(6.4)\[cdt' = \gamma_R(cdt - \beta_R dx)\]

(6.5)\[dx' = \gamma_R(dx - \beta_R c dt)\]

In particular, we note that if \(dx=0\) and therefore \(dt=dt_0\), then equations (6.4) and (6.5) simplify to

(6.6)\[dt' = \gamma_R dt_0\]

and

\[dx'=-\gamma_R\beta_R c dt_0 = -v_R dt' \rightarrow dx'/dt'=-v_R.\]

The first equation is Time Dilation, or that the time interval between two events in their rest frame is the shortest it can be, compared with any other frame in relative motion. The latter equation is simply indicating that if the primed frame is moving right, the events that were at rest will be measured to have moved to the left at the same speed.

The size of this four vector, also called the “interval” between the events, is

\[[dx_4]^2 = dx^2-c^2dt^2,\]

which in the rest frame reduces to \(-c^2dt_0^2\). The interval in the primed frame is therefore

\[dx'^2-c^2dt'^2,\]

or

\[ \gamma_R^2(dx - \beta_R c dt)^2- \gamma_R^2(cdt - \beta_R dx)^2\]

Plugging in the definition for \(\gamma_R\) and expaning the binomial squares:

(6.7)\[\frac{dx^2-2dx\beta_Rcdt+\beta_R^2c^2dt^2-c^2dt^2+2cdt\beta_Rdx-\beta_R^2dx^2}{1-\beta_R^2}\]

The cross terms cancel:

(6.8)\[\frac{dx^2+\beta_R^2c^2dt^2-c^2dt^2-\beta_R^2dx^2}{1-\beta_R^2}\]

regroup and pull out a factor of \(-\beta_R^2\):

(6.9)\[\frac{dx^2-c^2dt^2-\beta_R^2(dx^2-c^2dt^2)}{1-\beta_R^2}\]

Pull out the common factor and the \(1-\beta_R^2\) will cancel, leaving \(dx^2-c^2dt^2\), which is the same interval we started with in the unprimed frame! The interval does not change under the Lorentz transformation. This should of course be no surprise, because that is the condition under which we derived the elements of the matrix. In particular, the interval in the rest frame is therefore \(-c^2dt_0^2\), which means whatever the interval works out to be in any other frame, it must also end up being equal to \(-c^2dt_0^2\).

Hence, the size of the displacement 4-vector is an invariant under a Lorentz Transformation. Therefore, we say that it is a Lorentz scalar. It is interesting to note that the size of this invariant quantity is negative! This is quite different from the traditional 3 vectors used in Newtonian mechanics.

6.3. Muons in the Atmosphere

A good example of a system that has two clear events is the creation and decay of an unstable subatomic particle such as a neutron, lambda, pion or muon. The first event that is detected is the creation of the particle. At some later time (and perhaps displacement), the particle decays into something else. In the case of a muon, it decays into three particles: an electron, a mu-neutrino and an electron-neutrino:

(6.10)\[\mu^- \rightarrow e^- + \nu_\mu + \bar{\nu}_e\]

The experimentally measured half-life (the time for half of a large sample to decay) is \(2.20~\mu\)s as determined by an observer in the rest frame of the decay.

Consider this situation: D.H. Frisch and J.H. Smith report on an experiment they did ineasuring the flux of muons at the 6,300 foot summit of Mt. Washington (in New Hampshire) and at sea level in Cambridge Mass. At the top of Mt Washington, they measured the muon flux to be 568 muons/hour: When they used an identical apparatus down at sea levet in the lab at Harvard, they measured a flux of 412 muons/hour [Frisch and Smith, 1963].

The muons are produced when cosmic rays hit to upper limits of the atmosphere, A good assumption is that the rate of production of mesons at the top of the atmosphere is independent of time. The flux of muons then would be independent of time, but dependent on the altitude above sea level. The flux loss at sea level from that at the top of Mt. Washington is due to the decay given in Equation (6.10). Knowing the vertical distance between the two flux measurements and the half-life of the muon, the task becomes to determine the speed of the muons.

If Isaac Newton were to work this problem, he would calculate the time it took for the particles travel from Mt. Washington to sea level using the half-life and flux measurements. Then velocity = distance/duration. Particle decay rates are an exponentially dropping function,

(6.11)\[N(t) = N_0e^{-\ln{2}\frac{t}{halflife}}\]

The \(\ln{2}\) is to ensure that when \(t=\)halflife, then you have \(e^{-\ln{2}}\), which is 1/2. Given the flux numbers reported by Frisch and Smith, we can solve equation (6.11) for time to get:

(6.12)\[\Delta t = -\frac{{\rm halflife}}{\ln{2}}\ln{\left(\frac{N_{\rm sea level}}{N_{\rm Mt. Washington}}\right)} = -\frac{2.2\times 10^{-6}~{\rm s}}{0.693}\ln{0.725} = 1.0\times10^{-6}~{\rm s}\]

Now converting the altitude of Mt Washington to meters, the speed is

\[v = \frac{distance}{duration} = \frac{1920~{\rm m}}{1.0\times 10^{-6}~{\rm s}} = 1.9\times 10^9~{\rm m/s}\]

For this many muons to reach the earth, they must be traveling at more than 6 times the speed of light! How can that happen? Or, is Newton’s analysis wrong?

What is wrong with Newton’s analysis? The major problem is that the speed of the muons is close to the speed of light. So, the time that it takes for the muons to reach the surface of the earth in not the same for the observer that is at rest with respect to the muon as it is for the observer that is at rest with respect to the earth. We will have to use special relativity rather than the mechanics of dump trucks to work this problem.

There are two reference frames of interest, and they are graphed in Fig. 6.2. Let the unprimed reference (on the right) frame be the rest frame of the decay (where the observer is traveling at the same speed at the muons, and the Earth is racing toward the particle). Let the \(+x\) direction be “down” (towards the center of the Earth). The second observer (the primed observer) is at rest with respect to the Earth and the muon is moving quickly. The relative speed of the two reference frames \(\beta_R =-\)speed of muon. (The sign of the relative speed is negative since the apparent motion of the Earth is up toward the muon).

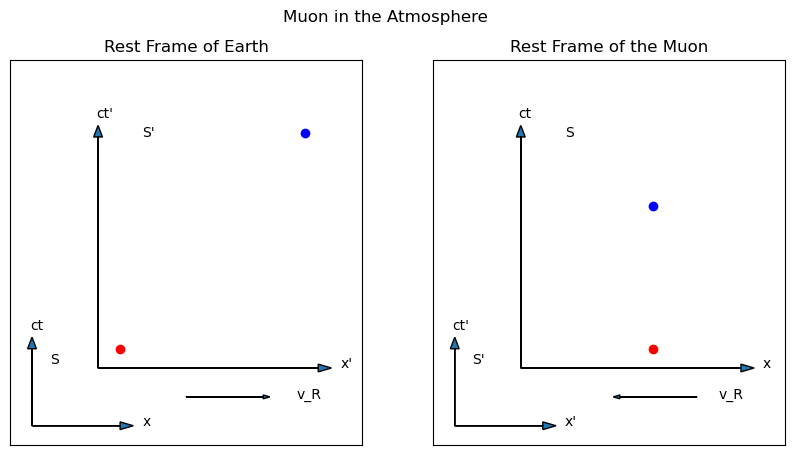
Fig. 6.2 Two spacetime diagrams to represent the creation of a muon in the upper atmosphere (red dot) and its subsequent decay at the Earth’s surface (blue dot). The unprimed frame (right diagram) is at rest with respect to the muon, while the primed frame (left diagram) is at rest with respect to the Earth. The primed frame is moving left (up in real space) with respect to the unprimed frame.

I know how far the particles have to travel in the rest frame of the Earth (\(\Delta x' = \)1920 m), and how long they live in the rest frame of the muons (\(\Delta t_0 = 2.2~\mu\)s). What I need to determine is the half-life of the muons in the reference frame that is at rest with respect to the earth, and how long it takes for the muons to reach the earth in the rest frame of the earth. To find the half-life in the rest frame of the earth, I need to find the displacement 4-vectors that each of the observers measure for the two events and use the Lorentz transformation to figure out the unknowns.

The two displacement 4-vectors for this problem are

(6.13)\[\begin{split}[dx_4] = \begin{bmatrix} ic 1.0\times10^{-6}~{\rm s}\\ 0.0~{\rm m} \end{bmatrix}\end{split}\]

The time as measured by the observer in the rest frame is correctly given by the analysis in Equation (6.12) as this observer does not observe that the muon moves with respect to him.

(6.14)\[\begin{split}[dx_4]' = \begin{bmatrix} ic dt'\\ 1920~{\rm m} \end{bmatrix}\end{split}\]

We set up the Lorentz transformation as per Equation (6.3)

(6.15)\[\begin{split}\begin{bmatrix} icdt\\ dx \end{bmatrix} = {\cal L}_x(-\beta_R) \begin{bmatrix} icdt\\ 0 \end{bmatrix} = \begin{bmatrix} \gamma_R & i\beta_R\gamma_R\\ -i\beta_R\gamma_R & \gamma_R \end{bmatrix} \begin{bmatrix} icdt\\ 0 \end{bmatrix}\end{split}\]

(6.16)\[\begin{split}\begin{bmatrix} icdt\\ dx \end{bmatrix} = \begin{bmatrix} i\gamma_Rcdt_0\\ \beta_R\gamma_Rcdt_0 \end{bmatrix}\end{split}\]

The second element in this matrix tells us that \(\beta_R\gamma_Rcdt_0\) must equal 1920 m.

(6.17)\[1920~{\rm m} = \beta_R\gamma_Rcdt_0 \rightarrow \gamma_R\beta_R = \frac{1920~{\rm m}}{c1.0\times10^{-6}~{\rm s}} = 6.40\]

(6.18)\[\gamma_R\beta_R = \frac{\beta_R}{\sqrt{1-\beta_R^2}} = 6.40 \rightarrow \frac{\beta_R^2}{1-\beta_R^2} = 40.96 \rightarrow \beta_R = \sqrt{\frac{40.96}{1+40.96}} = 0.988\]

Using the relativistically correct analysis gives a speed of the muon that is close to, but less than, the speed of light. Note what interpretation the experimental results seem to demand: for 73% of the muons at the height of Mt. Washington to reach sea level in Cambridge, it must seem to them that one microsecond has passed. But to cross 1920 m in one microsecond would require moving at a speed six times that of light. Therefore we deduce that the clocks in the muon’s frame are running slow, to give them more time to get to the ground. To match the observed data, the muons must be moving at 98.8% the speed of light.

Now this poses a further interpretive dilemma. One should be able to work this problem in either frame of reference, the one at rest with respect to the muons or the one at respect to the earth. In the frame that is at rest with respect to the muons, there is no time dilation – the one microsecond is the measured time interval. If the Earth is coming at the muon at 98.8% the speed of light, and is to reach the muon across 1920 m in one microsecond, the numbers don’t add up. But one of our postulates is that observers in both reference frames have to agree on what happens. The second event has to happen in both reference frames.

The only available parameter we can change, if the time and the speed are set, is the distance. The vertical distance between the top of the Mt. Washington and Cambridge must be smaller in the rest frame of the muon than the same distance as determined in the rest frame of the earth (1920 m), if the same physical results (fraction reaching Cambridge = 73%) are to happen. Not only does measured time depend upon which reference frame in which it is measured, but a measured length also must depend on the relative speed of the reference frame in which it is measured. The length must get shorter, or contract, when the relative speed between the two observers increases. This is called Length Contraction, and we will explore this effect in greater detail in the next section.

6.4. Length Contraction

To determine how length contraction happens, we will first find a method of converting a length measurement into two events as required by the model for special relativity. Then, we can use the Lorentz transformation to get between the two reference frames and see what happens to a length measurement.

Warning

This first step of converting a length measurement into two events is absolutely critical for understanding how length contraction works. One of the most common confusions around length contraction arises when people just assume they know the length of an object (remember in Chapter 2 we talked about the importance of not assuming you just know something going on elsewhere). It’s important to specify how you are measuring length, so you can be clear on how that process changes when you shift into another reference frame: the importance of operational definitions!

To create two events while measuring the length of an object, one method would be to choose a reference frame in which the the object is moving at a known velocity \(v_R\). When the front edge passes the observer creates a flash of light. That is the first event. When the back edge passes the observer, a second flash is created. A spacetime diagram for this process is shown in Fig. 6.3, where the worldline of the observer (at rest) is a red vertical line. The worldline of the front of the object is represented as a blue tilted line, and the worldline of the back of the obejct is a green tilted line. The slope of these lines is \(1/\beta\), where \(\beta\) is the speed of the object. The first event is where the green line crosses the red line, and the second event is where the blue line crosses the red line.

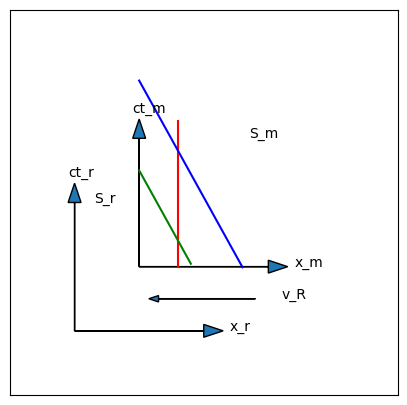
Fig. 6.3 A spacetime diagram that shows an object passing by an observer at rest. The red line is the world line of the observer. The green line and the blue lines are the front and back of the object, respectively. The object is moving to the left, at some speed \(v_R\).

The physical displacement as measured by this observer between the two events is 0.0 m (the observer has not moved). The time interval between the two events would be calculated as

(6.19)\[dt_0 = \frac{\ell_m}{-v_R} = -\frac{\ell_m}{c\beta_R}\]

where \(\ell_m\) is the deduced (measured) length of the moving object: the duration of time it takes to pass, multiplied by the speed of travel. The minus sign is because we have set this up with \(v_R\) going to the left, so it will have a negative value, but length is always positive concept.

As a four vector, we would write

(6.20)\[\begin{split}[dx_4]_m = \begin{bmatrix} -i\ell_m/\beta_R\\ 0.0 \end{bmatrix}\end{split}\]

and we drop the \(y\) and \(z\) components as not relevant.

Let the second observer be in the rest frame of the object whose length you wish to measure. This observer will see the same two events as the first observer, a flash occurring on the left edge of the object and at a later time, \(dt_{\rm rest}\), a second flash occurring at the right edge of the object. This observer is passing by the object as it is at rest, and this observer would interpret the physical displacement between the two events is the rest length of the object: \(\ell_r = dx_{\rm rest}\), where \(\ell_r\) represents the length of the object at rest.

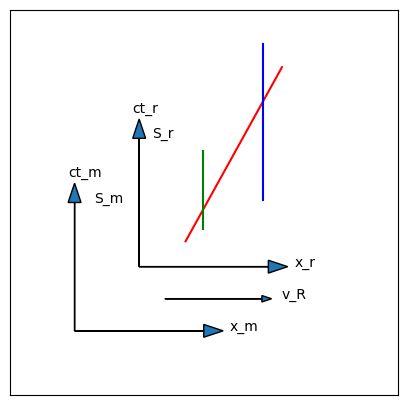
Fig. 6.4 A spacetime diagram that shows an observer passing by an object at rest. The red line is the world line of the observer. The green line and the blue lines are the front and back of the object, respectively. The observer is moving to the right, at some speed \(v_R\). Note that the lines in this diagram have been calculated by performing Lorentz transformations on points in the lines shown in Fig. 6.3 – they have not been simply redrawn.

When we write the four vector in this reference frame, it looks like

(6.21)\[\begin{split}[dx_4]_r = \begin{bmatrix} icdt_r\\ \ell_r \end{bmatrix}\end{split}\]

We can connect Equation (6.21) and (6.20) through a Lorentz transformation:

(6.22)\[[dx_4]_m = {\cal L}_x(\beta_R)[dx_4]_r\]

based on the diagram in Fig. 6.4.

(6.23)\[\begin{split}\begin{bmatrix} -i\ell_m/\beta_R\\ 0.0 \end{bmatrix} = \begin{bmatrix} \gamma_R & i\beta_R\gamma_R\\ -i\beta_R\gamma_R & \gamma_R \end{bmatrix} \begin{bmatrix} icdt_r\\ \ell_r \end{bmatrix}\end{split}\]

(6.24)\[\begin{split}\begin{bmatrix} -i\ell_m/\beta_R\\ 0.0 \end{bmatrix} = \begin{bmatrix} i\gamma_Rcdt_r + i\beta_R\gamma_R\ell_r\\ \beta_R\gamma_Rcdt_r + \gamma_R\ell_r \end{bmatrix}\end{split}\]

We want a relationship between \(\ell_r\) and \(\ell_m\), but there’s a \(dt_r\) in Equation (6.24) that we need to get rid of. We can set the second element to zero to get

\[cdt_r = -\frac{\ell_r}{\beta_R}\]

and then plug that into the first element:

\[-\frac{\ell_m}{\beta_R} = -\gamma_R\frac{\ell_r}{\beta_R} + \beta_R\gamma_R\ell_r\]

multiply through by \(\beta_R\) and factor out a \(\gamma_R\ell_r\) to get

(6.25)\[\ell_m = \gamma_R\ell_r(1 -\beta_R^2)\]

but the term in the parentheses is just \(1/\gamma_R^2\)!!! So we get that

(6.26)\[\boxed{ \ell_r = \gamma_R\ell_m }\]

In other words, as the object moves faster and faster, \(\gamma_R\) gets bigger and bigger, and therefore \(\ell_m\) (the length of the moving object) must get smaller and smaller, to keep the product equal to the value of the length of the object at rest. On the other hand, for very slow speds, \(\gamma_R\rightarrow 1\), and the two lengths become indistinguishable. This is, of course, why Newton never noticed such a thing.

It is important to be clear on your definition of length. The component \(dx\) is not always the length of the object. For example, in the “m” frame, the \(x\) component of the four vector is zero – this is not the length of the object. But if you define your operation by which you are measuring the length of the object in a particular reference frame, you will always find that it is shorter the faster the object is moving. See Chapter 5 for more examples.

Warning

We are often very casual when we talk about length contraction. Sometimes we talk about how long a passing object “looks”, or we might discuss what an observer “sees”. What we mean is what an observer in an inertial reference frame measures the length to be, using some procedure, like bouncing a laser and measuring the time interval, or measuring how much time passes for an certain spatial displacement, or some other specific procedure. What an observer would actually see (with their actual eyes), as an object zips by near the speed of light, would also depend on the light travel time to the observer from the object, how far the object moves in that time, and also the three-dimensionality of the object – its depth away from the observer.

A full treatment of these complications is beyond the scope of this book, but I will mention that it is possible to see the side of an object while the face is still toward you, because the front has essentially gotten out of the way of light coming from the back of the side. For dump trucks, the near corner would block that light, but for a fast-moving object, you could actually see around the corner, while the dimension along the line of sight contracts, and it would look (actually look) like the object was rotating. See, e.g. [Freund, 2008] or [Skinner, 1969] for a more detailed treatment of this topic.

6.5. Muon decay revisited

A second way of working the muon problem is to use the contraction of the measured vertical distance between the top of the Mt Washington and Cambridge as determined by the fast moving muon. According to Equation (6.26), the observer at rest with the muon measures the distance it has to travel to get to the surface of the earth to be:

(6.27)\[{\rm distance~to~Cambridge} = \frac{\ell_{\rm Earth}}{\gamma_R} = \frac{1920~{\rm m}}{6.478} = 296~{\rm m}\]

So, the muon thinks that it only has to travel 296 m to get to sea level. Now, from Equation (6.12), the muon thinks that it has traveled for 1 microsecond, so it calculates its velocity as:

\[\frac{296~{\rm m}}{1.0\times10^{-6}~{\rm s}} = 2.96\times10^8~{\rm m/s} \rightarrow \beta = 0.988\]

a value not different from the speed as measured by the observer on the Earth, calculated in Equation (6.18). In the frame of the Earth, the time is dilated, so the muons live longer and can reach the ground. In the frame moving with the muon, the distance to the ground is shorter, and therefore the muons can reach the ground in the shorter time they have. The events of being created and reaching the ground happen in both frames, but the reasons they can happen are interpreted differently in each frame.

6.6. The Ladder in the Garage Paradox

When people first grapple with length contraction, there is a common so-called paradox that often confuses them. Sometimes it refers to a pole in a barn, or a train in a tunnel, but I will use a ladder in a garage. The formulation of the “paradox” goes like this: consider a ladder that is 4 m long when it is at rest, and you want to try to fit it into a garage that is 2 m long when it is at rest. SR seems to say that if you run with the ladder at the garage with a speed of \(\beta=0.866\), then \(\gamma=2\) and the ladder will be contracted to only 2 m long, and can therefore fit into the garage. However, if you look at this situation in the rest frame of the ladder, the garage will be rushing at the ladder with a speed of \(\beta=0.866\), and will therefore be only 1 m long in this frame, so how can a 4 m ladder fit in a 1 m garage? The ladder can’t both fit and not fit in the garage!!! How can we resolve this paradox?

We can solve this dilemma through careful analysis of the relevant displacement four vectors and keeping in mind a clear, operational definition of what it means for one object to “fit” inside another.

Let’s retell this story in terms of events that we can plot on a spacetime diagram and then use to define some useful displacement four-vectors. Let’s start in the rest frame of the garage. The ladder is racing toward the garage, and the first important event is when the front of the ladder goes into the front of the garage. Let’s say we have two helpers, Frank and Betty, who are standing at the front and back of the garage, respectively. When the front of the ladder gets to the back of the garage, Betty opens a door that allows it to proceed without crashing into the wall. Meanwhile, Frank will close his door when the back of the ladder passes through the front door. If Frank closes his door before or at the same time as Betty closes hers, then the ladder can reasonably be said to be in the garage.

We now have four events we can plot on a ST diagram: the front of the ladder enters the front of the garage, the back of the ladder enters the front of the garage (and Frank closes the door), the front of the ladder arrives at the back of the garage (and Betty opens the door), and finally, the back of the ladder reaches the back of the garage. We will look at the borderline case, where Frank closes his door at the same instant Betty opens hers. The spacetime diagram is shown in Fig. 6.5, with four different color worldlines representing the front and back of the ladder and the garage. Our four events are the points where these four lines cross.

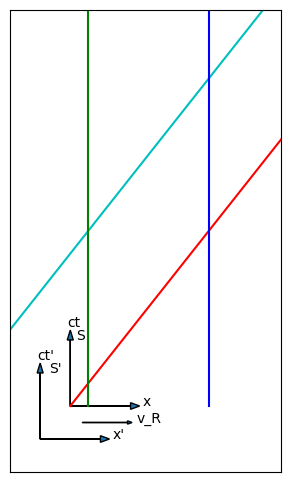
Fig. 6.5 A spacetime diagram showing a moving ladder passing through a garage at rest. The green line is the front of the garage while the blue line is the back of the garage. The red line is the front of the ladder, while the cyan line is the back end of the ladder. Reading up the time axis, the four events are: front of ladder enters from of garage (red crosses green), front of ladder reaches back of garage (red crosses blue), back of ladder enters front of garage (cyan crosses green), and back of ladder exits back of garage (cyan crosses blue).

In this reference frame, the ladder can be (barely) said to be in the garage. The red line crosses the blue line at the same time as the cyan line crosses the green line. For that brief instant, the ladder was in the garage. These four events give us at least four displacement four vectors, each of which defines one side of the parallelogram depicted by the crossing lines. Fig. 6.6 shows what happens when you apply the Lorentz transformation to these events, to shift them into the rest frame of the ladder.

In Fig. 6.6, the red and cyan lines have become vertical, confirming that the ladder is indeed at rest, while the green and blue lines tilt to the left. The green and blue lines are closer together than they were (1 m in this frame) while the cyan and red lines are further apart (4 m long ladder at rest).

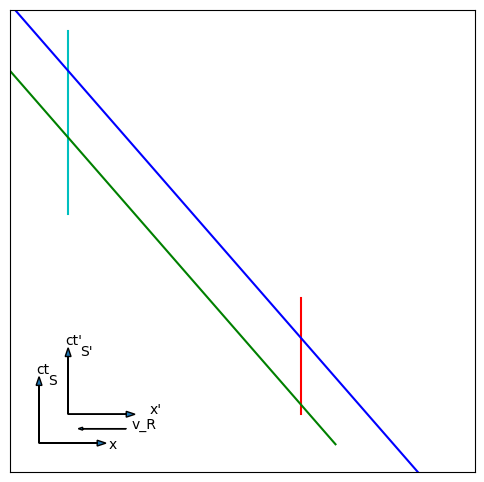
Fig. 6.6 A spacetime diagram showing a stationary ladder with a garage passing around it. The axes have been shifted four meters to the left to avoid crowding. The colors of the worldlines and the four events are the same as in Fig. 6.5, but note that these worldlines have been calculated via a Lorentz transformation. You must imagine the red and cyan lines extending indefinitely up and down.

Reading up the vertical axis, our four events as seen in this frame are: front of garage passes front of ladder (green crosses red), then back of garage passes front of the ladder (blue crosses red). Some time later, the front of the garage passes the back of the ladder (green crosses cyan) and finally the back of the garage passes the back of the ladder (blue crosses cyan). The garage slides across the ladder like a ring along a finger, and most of the time the ends of the ladder stick out both sides of the garage.

How can this be? Didn’t we say events have to happen in all frames? How can the ladder fit inside the garage in the first frame, but stick out both ends in the second?

The key to understanding why this is not a paradox resides in the definition of “fit in”. We defined the state of the ladder being in the garage as having both Frank and Betty close their doors at the same time. But you now know that simultaneity is relative. The “paradox” arose through a misunderstanding of what an “event” is. To say “the ladder is inside the garage” is not an event, and therefore is not required to happen in any reference frame. The events here are the ends of the ladder passing the ends of the garage. The events of the front of the ladder reaching the back of the garage and the back of the ladder entering the front of the garage are spacelike separated, and therefore nature makes no requirements as to what order they will occur in. All four events will happen, but not necessarily in the same order, so it is no paradox: the fact is that the ladder can fit inside the garage in one frame and not in another.

6.7. Problems

1. A beam of negative pions is produced in the lab, traveIing at \(\beta = 0.9980\).

a) What fraction of the original beam hits a target 200 meters away?

b) Show that this fraction is independent of which reference frame is used to do the calculation.

2. A beam of sigma plus particles is produced at the exit of a particle accelerator. The number of sigma particles left in the beam as a function of distance away from the particle accelerator is shown in Table Table 6.1:

Table 6.1 Sigma Beam

Number of Sigmas	Distance from Accelerator (cm)
257	5
175	10
130	15
100	20
87	25
65	30
52	35

Determine the speed of the sigma particles produced by the accelerator.

3. The nearest star to us is 4.600 light years away. A space ship traveling with \(\beta=.9980\) goes from Earth to this star.

a) How long does an observer on the earth measure the time for this trip?

b) How long does an observer on the space ship measure the time for this trip?

c) What distance does the observer on board the space ship measure the distance between the Earth and the star?

d) From the results of b) and c), what speed does the observer on the space ship calculate that the space ship is traveling?

4. Suppose that you are in the ‘rest frame’ of a photon. (Not possible, of course, but let’s try to imagine.) Also suppose that in the rest frame of the photon, it has a half life for decay to some unknown particle called \(\tau\).

a) write down the displacement 4-vector for a time interval of one half-life.

b) Use the Lorentz transformation to transform the displacement 4-vector for this decaying photon to a lab frame, that sees the photon traveling by at the speed of light (\(\beta_R = 1\)).

c) Determine the half-life of the photon as seen by an observer in the lab.

d) Is the photon stable? Why?

5. How fast must positive pion be traveling if it is to displace 20 m in the average life time of the pion? In the rest frame of the positive pion, the average life time of the particle = \(2.6 \times 10^{-8}\) s.

6. A friend of yours has a really hot car, it can travel at a speed of \(2.5 \times 10^8\) m/s. As this friend zips by you, you measure that the car is 5.00 m long and 1.57 m high. The measuring process took you 1.00 s.

a) What are the proper dimensions of the car, those that measured when the car is at rest with respect to the person doing the measurements?

b) How long did your friend think it took you to do the measurement? Which is to say, how long did your measurements take when measured by the friend? The friend agrees that you measured a time interval of one second – the question is what time interval does the friend measure?

7. A stick of length \(\ell_0\), laying in the \(x,y\) plane, makes an angle \(\theta\) with respect to the \(x\)-axis in the rest frame of the stick. A second observer, moving with relative velocity \(\beta_R\) in the \(+x\) direction observes this same stick.

a) What length does the second observer measure for the length of the stick?

b) What angle does the second observer measure between the \(x\)-axis and the stick?

9. A beacon light on a certain planet flashes once per microsecond as measured by clocks on that planet. In the frame of reference of a passing armada of Martians, the light moves 400 m between successive flashes.

a) In what direction do the Martians see the flashes displacing?

a) What is the speed of the armada relative to the planet?

b) What is the time between flashes as measured by the passing Martians. Note: be sure to set this up as a Lorentz transformation.

Warning

Don’t over think this. Simplify it to the terms used in this chapter. Don’t use \(y\) or \(z\) and don’t worry about light travel time between the planet and the armada.

10. In a certain reference frame, two events occur at the same place, but not at the same time.

a) Show that if event 1 precedes event 2 in this rest frame of the events, it precedes event 2 in all frames of reference: the temporal order of the events is invariant.

b) Comment briefly on the relationship of this result and the idea of cause and effect.