13. Concepts of General Relativity#
Although a full treatment of General Relativity (GR) is far beyond the scope of this book, I would like to leave you with some hints at the major concepts you must grapple with, if you extend the theory beyond the special case of reference frames moving with constant relative velocities. To help you get in the mindset the GR requires, and to help you realize how you need to challenge many assumptions that you previously thought were obvious, I cannot recommend highly enough the classic popularization [Eddington, 1920], which despite its age remains an insightful and illuminating presentation. The first chapter, in particular, is a three-way dialogue in the style of Galileo between three people representing three different ways of thinking about the world. By having them criticize each others’ positions, Eddington helps the reader understand assumptions about time and space that she would have otherwise taken for granted.
13.1. The Twin Paradox Revisited#
To begin our overview of GR, let us return to our old friend, the twin paradox, and consider the following situation: we have two events in the same location in space, one event later than the other in time. We have two individual clocks that have been syncronized, and they are both at the same location as the two events. At the instant of the first event, one of the clocks begins moving away. You could consider this to be the first event, if you like. The other clock remains stationary. At some later time, the clock returns to the location of the stationary clock. This return marks the second event. This situation is shown in Fig. 13.1, where the red line represents the worldline of the stationary clock and the blue curve represents a possible path that the moving clock might take. For our purposes, the exact path the moving clock takes is unimportant, only that it goes away and comes back. It must also, of course, be a physically possible trajectory: no doubling back along the time axis or moving faster than \(c\)!
From what we learned about SR, we can consider the displacement four-vector between the two events, and it would have a size given by \(-\Delta t_0^2\), the proper time between these two events, as measured by the red clock. However, it is not at all clear that the blue clock will measure the same time interval. Consider each worldline to be made up of infinitely many, infinitely small four-diplacements between events that are infinitesimally far apart along the colored lines. Each step along the worldline would have its own four-displacement, which would have its own size \(-ds^2=-c^2dt^2+dx^2\). For the purposes of this analysis, I am going to multiply through by \(-1\) and use \(ds = \sqrt{c^2dt^2-dx^2}\). It’s not strictly necessary, but it makes the argument easier to follow.
The total interval along each worldline would then be the integral of all the \(ds\) intervals for each of the steps.
Factor out the \(dt\) to make it easier to understand:
What we have here is a path integral of some function, call it \(f\), that depends on the speed of the clock at each moment along the path: \(f = \sqrt{1-v^2/c^2}\). For the red path, \(v=0\), so \(f=1\) and the integral is trivially just the proper time. However, along the blue path \(0\leq v^2<1\), so \(0<f\leq 1\), which means the result of this integral (which is the time interval elapsed on the blue clock, as we are integrating over \(dt\)) is always going to be less than or equal to the proper time. In particular, for the twin paradox, if the blue path were to involve traveling to some other star and back to the Earth, the clock on the spaceship (the blue clock) would measure less time than the clock on the Earth. This is the same result we derived before by only considering a one-way trip at constant speed.
No matter what path the blue clock takes, it will always measure less time than the stationary (red) clock. In this context, we can accurately say that moving clocks run slow, because we are comparing two clocks within the same reference frame. When we first encountered time dilation, we were considering the elapsed time between two events as measured by infinite lattices of synchronized clocks, one set being in motion relative to the other set. Back then, we said that the set of clocks at rest with respect to the two events would measure the shorter time interval.
In this context, within a single reference frame, we can say that a clock at rest with respect to two events will measure the LONGEST time interval between those two events, as compared with any other clock that follows a different path between the events. This sounds like it contradicts the previous formulation of time dilation, but you have to consider carefully what is being compared.
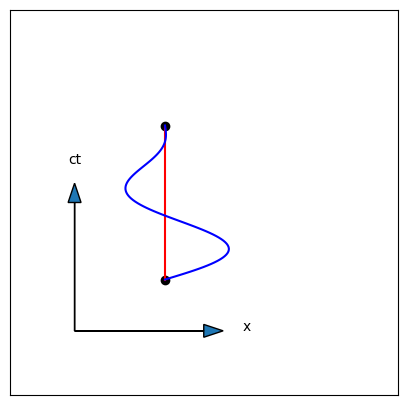
Fig. 13.1 Two events at the same place in a spacetime diagram, but showing two possible paths between them. The red vertical line is the worldline of an object at rest, while the blue line shows the path of a moving object that returns to the same place in time for the second event.#
In the first formulation, we were not comparing the time elapsed on two individual clocks. We were comparing two time intervals that were derived from collecting the clock readings on an infinite set of clocks, and then comparing the differences between the readings on the clocks closest to the events. In the reference frame in motion relative to the events, that meant two different clocks, which we assumed were synchronized and running at the same rate. In this new context, we are considering a single clock that moved away and came back to the original location.
In SR, there is no question of returning to the same location as the first event. This would not be possible, as to turn around and come back would require changing the relative velocity, and SR only considers unchanging relative velocities. In this new context, there is now an asymmetry between the moving clock and the stationary clock, because only the moving clock changes its motion. In the SR context, we could say that either reference frame could be considered moving or at rest (although only one reference frame would observe the two events at the same location), but in this context, there is no such symmetry. The only way to describe these occurances from the perspective of the blue clock would be to allow for accelerating reference frames.
13.2. Accelerating Reference Frames#
Imagine you are driving along in a car at a constant velocity. Everything in the car would behave according to Newton’s laws. Objects sitting on the dashboard would remain at rest (from your point of view – an observer sitting on the side of the road would see the objects moving at the same velocity as the car), and if you threw a ball into the back seat, you would see it move in a nice parabola. If you had a helium balloon, it would float upward to the length of its string. The fuzzy dice hang straight down from the rear view mirror. All is calm.
Then suddenly the driver slams on the brakes. The objects in the car fly forward. You feel thrown forward against the strap of your safety belt. The fuzzy dice swing forward toward the windshield. From your point of view, thinking in terms of Newton’s laws, a mysterious force has just appeared that gives all the objects in the car an additional forward velocity. What happens to the helium balloon? Take a moment to think about that and make a prediction. After you have decided, go to watch this video to see what the balloon actually does.
From the side of the road, there is no mysterious force. All objects continue moving forward, as their velocity would demand, but the car slows down, as does therefore the safety strap, which pushes backwards against you and slows you down to match the car. The balloon is lighter than air, so while the air in the car slides forward along with you and the fuzzy dice, that pushes the lighter balloon toward the back of the car.
If the driver had, instead of braking, turned the wheel hard to the left, so that the car began moving in a circle, everything in the car would behave as if there were a mysterious force pushing to the right. You would lean right, the fuzzy dice would dangle to the right, and the balloon would lean to the left. A person standing on the side of the road would say everything in the car was trying to go in a straight line, but the car was pushing it all to the left. Within the (accelerating) reference frame of the car, where no such leftward force is evident, everything would be acting as if a force to the right had suddenly appeared.
Let’s consider that circular trajectory in the context of Fig. 13.1. What if the blue path were to represent a clock moving in a circle and returning to its original location? What can we say about a clock that moves on a circular path through spacetime? Such a path is represented in Fig. 13.2. To get from the orange event to the purple event, a clock at rest would just follow a vertical line, but the black curve represents a clock that moves around in a circle. Based on the analysis of the previous section, such a clock would have to measure a shorter time interval than the clock at rest (if the system were sitting on a merry-go-round, we could consider the clock at rest to be at the center axis of the rotating disc – such a clock would be synchronized with the lattice of clocks making up the reference frame at rest with the orange and purple events, even if the clock at the center did not pass through those two events).
Fig. 13.2 3D spacetime diagram of an object moving in a circle in the xy plane. The worldline of the object is shown as a black curve. The object starts at the orange event and ends at the purple event. Both events are in the same place, but the purple event is later than the orange event. Rotate the diagram to see projections of the worldline onto the different planes. In particular, rotate the diagram to look straight down the \(ct\) axis to see the circular path in space.#
Within the reference frame of the purple and orange events (the clock at rest), for a given constant angular velocity \(\omega\), the larger the radius of the circle, the faster the clock will have to move to complete the circle (according to \(v=\omega r\)) and therefore the larger the discrepency in the time intervals, according to Equation (13.2). A clock further out on the merry-go-round will be moving faster and therefore measure a shorter time interval than a clock closer to the center. This would be very confusing to a person on the merry-go-round, as to that person, neither clock would be moving. The person on the merry go round would have to conclude that the stronger the centrifugal force, the slower the clocks run.
Furthermore, we also know that lengths contract at faster speeds, so if a person at the edge of the merry-go-round were to lay down meter sticks to measure the circumference of the circle, they would need more meter sticks than they would have expected without relativity. The radius of the circle, being perpendicular to the motion, is not affected, so \(2\pi r\) is now less than the actual circumference, according to the (contracted) meter sticks. See [Gamov and Stannard, 1999] for a nice illustration of this.
The circumference being equal to \(2\pi r\) is proven within a flat (also called Euclidian) space. If space is curved, that equation no longer holds. Consider the circle formed by a latitude line near the North Pole, as illustrated in Fig. 13.3: because the surface of the Earth is curved, the measured radius of the Earth along the surface is going to be longer than the radius of the circle you would get by slicing a flat circle along the latitude line. Therefore, the circumference of the latitude circle will be shorter than \(2\pi r\), because the Earth is curved. Due to the length contraction of the meter sticks, our scientist on the merry-go-round would also conclude that she is in a curved space, as the geometry is not behaving according to the rules of flat space, and the stronger the centrifugal force, the more curvature she measures.
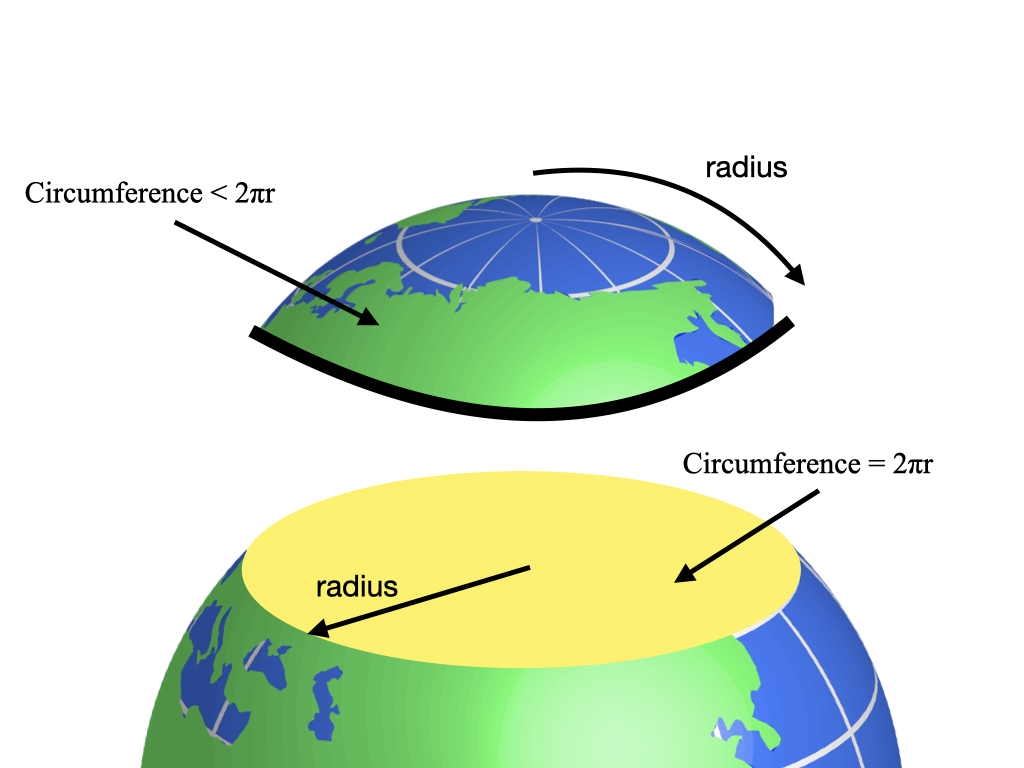
Fig. 13.3 Comparison of flat and curved geometry by slicing off a polar cap on the Earth. The flat surface formed by the cut has a circumference of \(2\pi\) times the radius, as you would expect. The curved surface of the cap has the same circumference, but an observer laying down meter sticks along a longitude line from the pole out to the edge would measure a longer radius than someone on the flat surface. They would therefore conclude the circumference is less than \(2\pi\) times the radius.#
The effects on time and geometry are tightly linked to the acceleration of the reference frame of the merry-go-round. The larger the radius, the larger the acceleration needs to be (\(a=\omega^2 r\)) to maintain the circular path. To someone on the merry-go-round, there would seem to be a mysterious outward (centrifugal) force, and to move toward the center would be to move “up” against this force, and to move away from the center would be to move “down” with this force. The further down they go, the larger the effects of time dilation and length contraction would get. They would conclude their spacetime was deviating more and more from Euclidean flatness. The same chain of logic holds for the acceleration due to gravity, because the forces are equivalent.
13.3. The Equivalence Principle#
Consider a rocket ship in deep space, far from any source of gravity. If that rocket were moving at a constant speed, everything in the rocket would drift around inside, because in the reference frame moving with the rocket, everything would be moving together, and would therefore be the same as if the rocket were not moving at all. This insight was first expressed by Galileo, although he talked about sailing ships, rather than rockets. It is only through the rocking of the waves, he pointed out, the deviations from constant speed, that we can tell the ship is moving. On our rocket, a laser affixed to one wall would shoot a horizontal beam straight across to the other side, regardless of the rocket speed, because the photons depart the wall with the same upward momentum as the rocket. Whether that upward velocity is zero or not, as long as it is constant, the result will be the same.
However, if the rocket is accelerating, the objects in the rocket will tend to “fall” to the floor. To an observer outside the rocket, watching the rocket accelerate on by, the objects are measured to be moving at a constant velocity, while the floor is accelerating up to meet them. Until they actually touch the floor, they are just drifting through deep space, unaware that anything else is happening. From inside the rocket, though, the objects seem to be moving down to the floor. If the rocket is accelerating up at 9.8 m/s/s, it will seem to anyone in the rocket that everything inside is experiencing a downward force exactly equivalent to the gravity on Earth.
This insight, that free-falling objects are no different from objects floating in deep space, was once described by Einstein as his happiest thought. The story goes that a painter in his town accidentally fell off the clock tower. The painter, who luckily survived, reported that he was just fine until he hit the ground. It occurred to Einstein that during the fall, the painter was effectively feeling no gravity. Only when he hit the ground could he tell that he was being accelerated. In the SR part of this book, we insisted on only dealing with reference frames moving at constant speed, which we considered to be “inertial reference frames”. However, a reference frame in gravitational free fall is also an inertial frame, because it is no different from a reference frame that is not moving in the absence of gravity.
There is a deep mystery in introductory Physics that is often glossed over, and perhaps not even mentioned. Gravity is introduced through Newton’s Law of Universal Gravitation, that any two masses in the universe attract each other in proportion to the product of their masses and inversely proportional to the square of the distance between them, or
Teachers have also by this point probably introduced Newton’s famous second law, often expressed that the total force on a system is proportional to the rate of change of the velocity of a system, with the constant of proportionality being called the mass, or
For a falling object near the Earth’s surface, these two forces are equated and the \(m\) term cancels out, indicating that the acceleration of any object near the surface of the Earth is the same, and we use \(GM/R^2\) with values for the mass and radius of the Earth to get \(g\equiv GM/R^2 = 9.8\) m/s/s. The velocity of any object falling near the Earth’s surface will change by 9.8 m/s every second, regardless of that object’s mass.
Buried in the chain of logic was a big assumption, so big and obvious that most students don’t even notice, and often are confused when it is actually pointed out to them: there is nothing in that description that demands that the two times \(m\) is used, they must be referring to the same thing. The \(m\) in Equation (13.3) is defined in terms of how strongly masses pull on each other through gravity. The \(m\) in Equation (13.4) is defined in terms of how much an object’s velocity changes when you push on it. There’s nothing in those two definitions that says those two have to be the same thing! It’s a huge assumption and a complete mathematical slight of hand trick to define them with the same letter \(m\) in the first place.
Einstein’s theory of General Relativity insists that they are indeed the same thing, and provides a reason why that might be the case. If what we call gravity is indeed a kind of illusion caused by being in a curved spacetime, then falling objects aren’t really falling, but rather just drifting through spacetime as they normally would, until the ground, or the floor of the rocket, comes up from below and hits them. Everything falls at the same rate because everything is drifting together through a curved spacetime. GR suggests that you will never be able to do any experiment to be able to tell the difference between these two situations (standing on the Earth vs. standing on the floor of an accelerating rocket), because they are equivalent.
Consider again the accelerating car. However, now imagine the car is parked. Everything in the car will behave according to Newton’s laws: the dice will hang down, the safety strap will not press against you, and the balloon will rise straight up to the top of its string. If, now, the Incredible Hulk were to grab the back of the car and lift it up, such that the car were tilted at a large angle, consider what would happen inside the car: the dice would shift forward, you would feel pushed against the safety belt, and the balloon would tilt back toward the back of the car. An observer outside would say everything is simply staying oriented to gravity’s “down”, but inside the car, it would seem like a mysterious force was pushing foward, exactly as if the driver had slammed on the brakes. In fact, if the two kinds of mass are truly equivalent, there is absolutely no difference between braking the car and tilting the car. In one case, we would say a mysterious “fictional” force was adding a horizontal compontent to the total force on objects in the car, and in the other case, we would say that the force of gravity was rotating, so that it gained a horizontal component that wasn’t there before. In both cases, the total force vector, from the point of view of everything inside the car, would swing from vertically down to diagonally down and forward.
There is a very simple demonstration one can perform that illustrates how an object in free fall near the Earth’s surface is equivalent to the object floating in deep space. If a bottle of water near the Earth has a hole in the side, gravity will pull the water downward, but the bottom of the bottle will push back against the water, and the water will squirt out the side. If the bottle were floating far away from gravity, there would be no reason for the water to squirt out the hole, and it would simply stay in the bottle. Therefore, if the Equivalence Principle is valid, water should stay inside of a bottle in free fall near the Earth. In the short video included here, a bottle of water is suspended from the ceiling, generating a stream out a hole in its side. At about five seconds in, the string holding the bottle is cut. You will note that the water stops streaming out and both the top of the already moving stream as well as the bottle itself fall at the same rate thereafter.
This insight is so important that this “Equivalence Principle” occupies a similar place in the foundation of GR that the two postulates of SR do for that theory. Within the formulation of GR, what we would normally (in Newtonian mechanics) consider to be a force that we call “Gravity” is instead interpreted as an illusion of objects trying to move through curved spacetime, just like we infer forces to explain the motion of the balloon and the fuzzy dice in the accelerating car.
In this sense, gravity is not really a force, but it gives the impression of causing acceleration because objects in free-fall are drifting through curved spacetime. Any observer drifting along with those objects will observe no apparent forces acting on anything. Astronauts in orbit drift around their capsules as if there is no gravity, although Newton would say that they and their spacecraft and everything around them are absolutely being pulled on by the Earth. They are in free fall. Any experiments you might carry out inside the falling bottle in the video, above, would yield the same results as the same experiment carried out in a bottle floating in deep space with no gravity.
If you are sitting calmly in a chair on the ground, you would think you are not accelerating. However, relative to a falling inertial frame, like a painter falling off a clock tower, you would be measured to be accelerating upward. Therefore you feel the chair pushing up against you. That is what is pushing you upward, stopping you from joining in the freefall that the curved space around you would demand. You don’t feel the gravity – you feel the chair. If someone were to pull the chair out from under you, you would be like the falling painter. Until you hit the ground, you would feel no gravity. As long as you are sitting in the chair, it’s just as if you were in that accelerating rocket, pushing up against you. The situations are equivalent.
Note
One of the weirder implications of the equivalence principle is that \(E=mc^2\) really runs both directions. Energy has a gravitational effect, despite not really existing in space. Consider, for example, atomic nuclei. The rest energy of, say, a carbon 12 nucleus is less than the rest energy of six protons and neutrons. We associate a “binding energy” with the strong interaction that holds these particles together as a nucleus. For C12, that’s about 92 MeV. A proton has a mass of \(1.672623\times10^{-27}\) kg, and the neutron has \(1.674929\times10^{-27}\) kg. The mass of a C12 nucleus is about \(1.99265\times10^{-26}\) kg. Add the mass of a proton to the mass of the neutron and multiply by six and you get \(2.0085\times10^{-26}\) kg. The bound nucleus has a lower energy and therefore a lower mass, and therefore less gravity than six protons and six neutrons would on their own. A cup of hot water loses thermal energy as it cools off, and therefore would have less mass and less gravity at lower temperature (although the mass loss due to steam rising off the water would be much greater).
13.4. The Pound-Rebkha Experiment#
If the Equivalence Principle is valid, than any situation where the acceleration of a reference frame changes should have equivelent inertial effects and gravitational effects. There should not be any way to distinguish between them. In particular, consider the merry-go-round described in the previous section. The further out you go along the radius of the rotation, the more acceleration you would experience, and the slower your clocks would be running, compared with a clock at the axis. The centrifugal force is therefore equivalent to gravity, with “out” being “down” and “in” being “up”. Therefore, a clock that is further “down” in gravity (closer to the Earth) should run more slowly than a clock that is further “up” (away from the Earth).
The frequency of a photon is a perfectly good clock – it oscillates in time and therefore can mark off the nanoseconds as well as any other clock. If we shine light upward from the surface of the Earth, its frequency should decrease as it goes upward. If we detect the photon at a higher altitude, we will perceive it as a lower altitude clock that is running more slowly, as per the arguments in the first few sections. This “gravitational redshift” can also be understood in terms of energy: if you throw a ball upward, it loses energy as it climbs. The ball’s energy manifests in its speed. The rising ball slows down. A photon cannot slow down – it loses energy by shifting to a lower frequency. This is yet another counter-intuitive way that a massless particle acts in ways that we previously only associated with mass. We can’t calculate the potential energy of the interaction of the Earth and a photon in the same way that we would the interaction of the Earth and the ball: \(mgh\) makes no sense for the photon. However, we have learned the photon has momentum despite having no mass, so perhaps it is not so surprising that it can lose energy in climbing upward, too.
To try to put this into quantitative form, let us consider the energy of a photon, proportional to its frequency: \(E=hf\). If this energy has an equivalent inertia to \(E/c^2\), then we would expect the energy of the photon to drop by \(dE = -Eg(dy)/c^2\) as it moves a height \(dy\) up from the Earth’s surface. Divide both sides by \(hf\) to get
For reasonable distances (\(\sim 10\) m) near the surface of the Earth, this consititutes a fractional frequency shift of \(\sim 10^{-15}\). This is a very, very tiny change, and very difficult to measure.
In 1960, Robert Pound and his student Glen Rebkha at Harvard set out to measure this tiny shift. They positioned a source of X-rays (X-rays with a well-known frequency) at the bottom of of a tower, and a detector at the top of the tower, 21 m above. It would be impossible to measure a fractional shift of one part in a thousand trillion directly, so they positioned a filter in front of the detector. The filter would only allow X-rays through if they matched the original frequency of the emitted X-rays from the source.
They set the filter on a vibrating frame. By controlling how the filter oscillated up and down, they could cycle through many relative speeds between the filter and the source of X-rays. From the reference frame of the filter, the X-rays would be Doppler-shifted. When the filter was moving upward, the Doppler shift would be a redshift, and when the filter was moving downward, the Doppler shift would be a blue shift. At just the right downward speed, the Doppler blueshift would cancel out the gravitational redshift and allow the X-rays through to the detector.
Such a short description makes it sound easy, but only because the gory details are beyond the scope of this book. Pound and Rebkha performed many runs over years, refining their measurements and paying careful attention to sources of error. See, for example, the Wikipedia page about the experiment. Their first ten-day run reported a gravitational redshift of \(-(2.56\pm0.25)\times10^{-15}\), a 10% uncertainty which they were able to eventually refine down to 1%. Think about that! Such a small difference is equivalent to two clocks losing only one relative second over a 15 million year time interval!
13.5. The Weight of a Box of Photons#
This gravitational redshift leads to an interesting thought experiment. Back in Chapter 8, the last problem asked you to consider a box of photons and whether those photons might have an inertia equivalent to some amount of mass. Hopefully you figured out that the inertia came from reflecting the photons off the inside walls of the box. If you wanted to move the box, say to the right, then the photons bouncing off the left (approaching) wall must pick up energy/momentum, and the photons bouncing off the right (receding) wall must lose energy/momentum. By conservation of momentum, you will measure a force resisting your pushing the box, as if the contents of the box had mass.
The same result applies to a box sitting on the ground in Earth’s gravity. The photons travelling upward will lose energy according to Equation (13.5), such that on average they will have a energy loss of \(-Egy/c^2\) relative to the ones hitting the bottom of the box, and therefore a momentum difference of \(-Egy/c^3\). There’s no change in the horizontal directions, so I only need to consider the photons going up and down – sideways motion will average out to zero.
Consider a patch of the bottom and top sides of the box with area \(A\). In a time \(dt\), a certain number of photons will hit that patch: the density of the photons in the box \(n\) times the volume \(Acdt\). Each of the photons that hits a side of the box will impart an impulse of twice its momentum so the total impulse delivered to the box will be the difference between the bottom and the top: \(nAcdt\times Egy/c^3\). (There is a factor of two from the reflection that cancels out when you consider that the photons are not traveling straight up and down. Integrate over all possible angles to get a factor of 1/2.) Divide through by \(dt\) to turn impulse into force. Then note that if you take \(A\) to be the total area of the top and bottom of the box, then \(nAy\) is just \(N\), the total number of photons in the box.
This leaves the total force on the bottom of the box to be \(-NEg/c^2\), which is just what you expect if each photon has an equivalent mass of \(E/c^2\): the total mass of the photons would be \(m=NE/c^2\), so the total force pushing down on the floor below the box would be \(mg\). However, this is not from applying a gravitational force, in the sense of \(mg=GMm/R^2\), but from considering the gravitational redshift of photons moving upwards in the curved spacetime around the Earth’s mass.
13.6. Einstein’s Equation#
Within the context of General Relativity, the Equivalence Principle becomes not only understandable, but inevitable. Instead of a mysterious coincidence, that gravitational mass and inertial mass just happen to be not different from each other, gravity itself is reconceptualized as an inertial effect of curved spacetime, and therefore the masses must be the same.
If gravity is just an inertial effect of the curvature of spacetime, and the correspondence principle demands that GR reduces to Newtonian physics in the limit of small masses and large distances, then there must be a link between the presence of mass and the curvature of spacetime. Newton’s Law of Gravitation describes how objects with mass exert forces on each other across space. It suggests no mechanism for how this might occur, and it is helpless against the challenge of the speed of light limit to the universe – how can the Earth pull on the Sun from where it is now, rather than where it was eight minutes ago, the time it takes light to travel from the Earth to the Sun? This question would have never occured to Newton, but once Relativity demands a universal speed limit, the question must be answered.
Einstein’s General Relativity provides a new set of equations that replace Newton’s gravity with a formalism that shows how the presence of mass (and indeed energy as well) is linked to the curvature of spacetime, which in turn manifests as apparent forces that we call gravity. As John Wheeler once said, Einstein’s Equation means that “matter tells spacetime how to curve, and the curvature of spacetime tells matter how to move.”
An actual derivation of Einstein’s Equation is beyond the scope of this introduction. Suffice to say that it involves writing down the distribution of matter and energy in space as a \(4\times 4\) tensor, and then linking that tensor to spatial and temporal rates of change of spacetime. It is not inappropriate to compare Einstein’s equation to Poisson’s Equation in Newtonian Gravity:
which says the curvature of the gravitational potential is proportional to the amount of mass in a given location. There is an identical equation linking the curvature of the electric potential to the amount of charge in a given location. In both cases, the force connected to the material (gravity to mass, electric force to charge) is the slope of the potential curve. Einstein’s equation therefore is saying that the curvature of spacetime is directly linked to the curvature of the gravitational potential, and that helps us see how a force could be connected to the curvature of spacetime.
So Einstein’s equation links the curvature of spacetime to the matter and energy that are in a given location. To solve it, you specify some distribution of matter and energy, and ask what kind of spacetime curvature is consistent with the equation. The form such a solution takes is the metric of the spacetime that we associate with a particular kind of distribution of matter and energy.
13.7. Metrics#
If we are to follow a curved path through spacetime, or a path through curved spacetime, we need to be able to write down the interval between two events with an infinitesimal four-displacement. A path length is an integral over many tiny steps, and if we are to actually calculate it, we need to be able to know how two nearby events in spacetime are related to each other.
In flat space, one would simply say the distance between two points is given by the Pythagorean theorem: \(ds^2 = dx^2+dy^2+dz^2\). If we extend that concept to spacetime, we get \(ds^2 = -c^2ct^2+dx^2+dy^2+dz^2\). As explained in Chapter 3, we can use the concept of the metric to write this sum of squares as the inner product of two four-vectors:
where \(g_{\mu\nu}\) is the metric of the spacetime. For flat spacetime, the metric is simply given by Equation (3.5), which I repeat here:
In principle, if spacetime were curved, these numbers would not all be \(\pm1\) or zero. For example, if you were using spherical coordinates in three-dimensional space, you could use \(dx_j = [dr~d\theta~d\phi]\) and then the \(3\times 3\) metric would be
The fact that the numbers on the diagonal are not always one tells us that a sphere is not flat.
The metric contains all the information we might need to know about the distribution of matter/energy in a given volume of spacetime, because the shape of the metric is determined by the distribution of matter/energy according to Einstein’s equation. In the same way that the electric field tell you where the sources of electricity are, the metric tells you where the sources of gravity are. There is more about the metric in Chapter 3, and we will return to a few special metrics of interest in Chapter 14.
13.8. Geodesics#
How can we understand this perplexing fact that a reference frame locked to a painter in constantly accelerating free fall is also an inertial reference frame? We need to widen out our definition of what kind of relative motion still allows a reference frame to be inertial. In Chapter 2, we insisted that reference frames move at constant relative velocities. In flat spacetime, such a reference frame is definitely inertial. But in curved spacetime, that special case is no longer applicable. If you were falling near the Earth, but you wanted to move in a straight line at a constant velocity, you woud need to find a way to exert forces on yourself. Otherwise, you would fall at an ever-increasing speed (until you hit the ground).
In Newtonian Physics, we say that an object experiencing no net force will maintain a constant velocity. We need to modify that statement to allow for curved spacetime. The equivalent statement is that objects experiencing no net force will follow a path in spacetime that maximizes the time as measured by a co-moving clock. Such a path is called a geodesic.
Note
It is worth taking a moment to recall the operational definition of “proper time”. The requirement that the proper time be a maximum can be confusing in the light of how we defined time dilation. In Section 3.4, we established the proper time as the minimum time interval between two events, as measured by a lattice of clocks at rest with respect to those events. There are two clock readings, measured on different clocks, and we take the difference to get the proper time interval. Since the reference frames we were considering were all moving at constant relative velocities, it was easy to imagine straight lines between these events, and to consider the difference in clock readings as telling us the vertical lengths of those lines on a space-time diagram. However, the way we are defining proper time here is a little more subtle. We are breaking a not-necessarily-straight wordline up into infinitely many, infinitely small, intervals, each of which can be considered to be approximately straight, and measuring the difference between two clock readings on the same clock, as it moves from one event to the next. In the (possibly accelerating) rest frame of that clock, the sum of all those tiny time intervals would be not different from the proper time, as we understood it in Section 3.4. Allowing the clock to accelerate yields a different numerical answer, while preserving the same operational definition as in the non-accelerating case. We can then talk about finding the path that maximizes the proper time, a process which is unrelated to the previous discussion of time dilation. Here we are discussing alternate paths and comparing multiple proper times; time dilation is a comparison of a single proper time to a different time interval measured in a reference frame in relative motion. The proper time is the maximum time interval when comparing all the possible paths between two events, but it is still shorter when the two events are at rest when compared to the time interval in a reference frame where the two events are not at rest. These two definitions do not contradict each other, because they are considering different comparisons.
A photon is an ideal object to use as a test case, because a photon has no mass, and can therefore never experience a force, and will always follow a geodesic path. In fact, we can often determine what the geodesic is, and therefore whether the space around us is flat or curved, by studying the paths that photons take. As illustrated in Fig. 13.1, and explained in the first section, in a flat spacetime, the path that maximizes the proper time between two points is a straight line trajectory. In a flat spacetime, objects experiencing no net force will either remain at rest or move at a constant velocity. For an object’s path through spacetime to deviate from a geodesic, a force must be exerted on it.
In practice, to figure out the geodesic between two events in a curved spacetime requires maximizing the proper time over all possible paths between the two events. In calculus, we learn how to maximize a function over a variable: take the derivative and set it to zero. However, how to differentiate with respect to a path is more complicated, and requires a branch of mathematics called The Calculus of Variations, which is beyond the scope of this book. However, we can use some approximations and work through one simple example to show how this sort of approach can work.
Let’s consider an object like a baseball, moving through the curved spacetime near the surface of the Earth. We want to find the geodesic path between two events \(A\) and \(B\), where both \(A\) and \(B\) are at the same location in space, but \(B\) is at a later time than \(A\) (the spacetime diagram in Fig. 13.1 applies here, too, with \(A\) being the lower dot and \(B\) being the upper dot. Take the horizontal axis to represent the height, \(x\)). We know from classical introductory mechanics that the ball will follow a parabolic trajectory such that \(x(t) = x_A + v(t_A)t-1/2 g t^2\). At \(t=0\), the ball is at a height \(x_A\), and if the ball is to return to \(x_A\) at the time of event \(B\), it has to be given the right initial velocity. Too slow, and it will return before event \(B\), but too fast, and it will not be back yet by the time event \(B\) happens.
We therefore know that the geodesic should be a parabola in space. Can we understand this result within the formalism of relativity? We need to modify Eq. (13.1) to include the curvature effects near the surface of the Earth, using Eq. (13.5). If the object increases in altitude by \(dx\), going from \(x=0\) to \(x=dx\), the clocks will all run slower by \(gx/c^2\), going from \(dt\) to \(dt(1+gx/c^2)\). As explained in the merry-go-round example, above, rulers will also shrink as you go up, so the length of an interval \(dx\) will also grow, and by the same factor.
If we multiply out \(ds^2\), we get a new version of Eq. (13.1):
take the square root and factor out the common factors to set up the integral over the path to get the proper time \(\Delta t_0\):
as long as \(x(t=0)=x(t=T)=0\). In so far as \(g\) is small but not zero, the spacetime is curved away from flatness. Note that for the Earth, \(g/c^2\) is about \(10^{-16}\) 1/m, a very small number.
Next we make the approximation that no baseball is going to go anywhere near the speed of light, so \(v\ll c\) and we can replace the square root with a linear approximation:
Next we multiply the two binomials and drop second order terms:
This is technically as far as we can go without the Calculus of Variations. To solve this integral, we would need some function of \(x(t)\), which would define the path. Then we could take \(v=dx/dt\) to be able to get the second term into a functional form we could integrate. While I can’t prove that a parabola gives the largest possible proper time interval of all functions \(x(t)\) that go through \(A\) and \(B\), I can show that a parabola yields a bigger proper time interval than just sitting still.
For a baseball sitting still, both \(x\) and \(v\) are zero, so the integral is just \(T\). For a parabolic path with an acceleration \(-a\), the path would have to be \(x(t) = v_0t - 1/2 at^2\), and therefore \(v(t) = v_0-at\). So the path integral becomes
Multiply everything out to get
Regroup by like powers of \(t\):
and integrate:
At this point, we can use simple calculus to ask what value of \(a\) will maximize \(\Delta t_0\)? In other words, of all the possible parabolas that go through \(A\) and \(B\), which value of \(a\) will maximize the proper time? That doesn’t prove anything about all possible paths of any shape, but it’s the best we can do without Calculus of Variations.
We need to differentiate Eq. (13.16) with respect to \(a\) and set to zero. But we also know from the path equation that for the ball to come back down in time (\(x(T)=0\)), \(v_0 = aT/2\). Plug that in first:
which demands \(a=g\)!
Of all the possible parabolic paths between \(A\) and \(B\), the one with \(a=g\) will maximize the proper time elapsed between \(A\) and \(B\). The math represented here symbolically is also shown graphically in Fig. 13.4. You can move the slider to change the acceleration, while the graph shows the spacetime trajectory and the number in the box represents the size of the deviation between the time interval for the parabolic path and that of an object at rest (set acceleration to zero and the number in the box will also go to zero). You can see that the largest deviation in time is when \(a=9.81\) m/s\(^2\).
Fig. 13.4 3D spacetime diagram of an object moving in a parabola near the surface of the Earth. The \(x\) direction represents the vertical and the \(y\) direction represents the horizontal. With the slider you can change the acceleration. The ends of the parabola are fixed to the start and stop events. The black number in the box represents the deviation of the proper time along the parabolic path from the proper time for an object at rest between the two events, in arbitary units. You should be able to see that the time takes a maximum when you set the acceleration equal to \(g\) (\(-9.8\) m/s\(^2\)).#
It remains to be shown that the parabolic path has a larger proper time than the straight line path (you can see this in the number in the box in Fig. 13.4, but we should show the equations for it). For this, we return to Eq. (13.16) and plug in \(a=g\) to see what the proper time is along the parabola:
Since the term on the right is always positive, this proper time will always be bigger than \(T\), which is the proper time for a ball sitting still the whole time. In the presence of a weak, uniform gravitational field, the parabolic path will have a larger proper time than the straight line path, which means the ball will not follow the straight line path. However, if we remove the gravitational field by setting \(g=0\), then the geodesic will be a straight line – it reduces to the special case as the correspondence principle demands. I have not proved that the parabolic path maximizes the proper time out of all the possible paths between \(A\) and \(B\), but it is certainly a larger time than sitting still, in the presence of uniform gravity.
In other words (accepting provisionally that a parabola does indeed maximize \(\Delta t_0\) out of all possible paths), if no forces are acting on the ball, it will follow a parabolic path between \(A\) and \(B\), simply by moving along a geodesic. If you want the ball to travel a different path, say not moving at all, you will have to exert a force on it. For example, if the ball is lying on the ground, the force from the ground will push upward and keep the ball from falling down. The geodesic path therefore represents the natural trajectory through spacetime, in the absence of forces. All objects following geodesics will, within a reference frame moving with them, to be experiencing no net forces. That reference frame is therefore inertial.
The reference frame that is not in free-fall near the Earth (for example, the reference frame at rest with respect to the ground) is not inertial, in this sense, because we need to invent a force to explain why everything seems to accelerate downward when released, and we call that force gravity. Much like if we were in a rotating reference frame, we would need to invent a centrifugal force to explain why everything moved away from the axis of rotation. However, in a flat spacetime, the geodesic is a straight line at constant velocity, which is why up until this chapter, when considering inertial reference frames, we insisted on the special case of constant relative velocities, thereby distinguishing special relativity from general relativity.
13.9. Summary#
Putting your brain into the mindset of the General Theory of Relativity requires a radical reconceptualizing of space, time, motion, and gravity. From within the paradigm of GR, gravity becomes another fictional non-inertial force, much like the centrifugal force, or the force that seems to push us forward when we step on the car’s brake pedal. In this interpretation, gravity is equivalent to such a force, and this Equivalence Principle explains why the gravitational and inertial masses of objects seem to be equal.
The presence of matter and energy, as described by Einstein’s Equation, determines the local curvature of spacetime, and in the absence of other forces, objects will follow the paths through that spacetime that maximize their own elapsed proper time. These paths are called geodesics, and for an object to deviate from a geodesic, a force must be applied. This is how to reconceptualize Newton’s First Law away from flat space into possibly curved spacetime. This leads to conclusions that seem absurd on their face: that a free-falling painter is not accelerating, while a ball sitting on the ground is. That clocks speed up at higher altitudes, and light rays coming from close to massive objects will lose energy and be redshifted.
Despite the conceptual challenges, GR has so far passed every test to which it has been subjected. This chapter has already mentioned the Pound-Rebkha experiment, and the next chapter will explore the precession of Mercury and the existence of gravitational lensing. In addition to these observational tests, theorists exploring the implications of the theory have led to some of the most exciting ideas in the Universe, such as Black Holes and the Big Bang Theory itself. We will explore some of these in the next and final chapter.
13.10. Problems#
Project GREAT. In 2005 Tom Van Baak carried out a home experiment in General Relativity. He carefully synchronized six precise computer clocks and then took three of them on vacation with his family, 1340 m higher on Mount Rainier. They spent two days (48 h) at this higher elevation and then returned home. How much time difference would you expect there to be between the two sets of clocks upon their return? Which clocks would be ahead? Once you have made your prediction, you can read their report here.
One of Einstein’s original predictions from GR was that light leaving the Sun should be redshifted. It turns out this is much harder to measure than you might think, not least because the solar “surface” is in motion, so the light is Doppler shifted as well as gravitationally shifted. Based on your reading here, how much would you expect the wavelength of a photon from the Sun to change by the time it reaches the Earth? The best measurement (so far) of this effect was reported by Hernandez et al. in 2020.
GPS satellites provide accurate locations to receivers on the Earth by broadcasting a time signal. The time intervals from multiple satellites, combined with the speed of light, pinpoint the receiver’s position. The satellites are roughly \(2.02\times10^6\) m above the Earth’s surface, circling the Earth twice a day. From this information, estimate how much faster the GPS clocks are than our phone clocks here on the ground, and how much slower they are from the time dilation due to their speed. Express your answer in units of microseconds per day. These effects must be compensated for, if the GPS system is to provide accurate locations.
Show that that the extremum for \(\Delta t_0\) at \(a=g\) is indeed a maximum and not a minimum or inflection point.