4. Lorentz Transformations

We have already seen that requiring the size of a four-vector to be invariant across reference frames leads to interesting implications (time dilation, for example). However, there are more insights that can be gained by figuring out a method to predict what the components of a four vector will be in a second reference frame, given measurements of that four vector’s components in a first reference frame. The change of a four vector from one reference frame to another with a constant relative velocity is called a Lorentz Transformation.

4.1. Setting Up the Problem

The Lorentz transformation converts the components of a 4-vector in one inertial reference frame to the components as measured in a second frame moving at a constant velocity relative to the first. This method works for any four-vector, but we will define it using the displacement four-vector, as that is easy to visualize.

We start by recreating Fig. 3.2 as Fig. 4.1 – to make sure you are applying the transformation properly, it is useful to always start by recreating this diagram and making sure that you are assigning the correct numbers to the elements, as defined in this diagram.

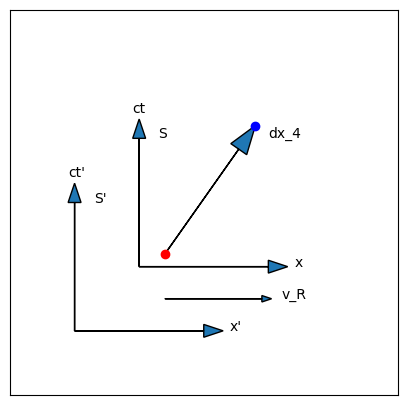
Fig. 4.1 The spacetime diagram that defines a Lorentz transformation. There are two events, indicated by red and blue dots, and we define a displacement four vector between them (indicated by an arrow). These components are defined in the reference frame \(S\), and we want to know the components in a second frame \(S^\prime\), which is moving with a constant relative velocity \(\vec{v}_R\). We define \(x\) such that it lies parallel to \(\vec{v}_R\).

The 4-vector components are determined by the two events shown as colored dots in Fig. 4.1. Since we have the choice of which is the x-axis, we will always pick the relative velocity of the two observers to lie along the \(x\)-axis, to make the math simpler. Putting the diagram of Fig. 4.1 into 4-vector notation, we need a tool that will take us from \([dx_4]\) to \([dx_4]^\prime\), like so:

(4.1)\[[dx_4]^\prime = {\cal L}_x(\beta_R)[dx_4]\]

The Lorentz transformation can be mathematically represented as a matrix, because it transforms one vector into another. The Lorentz transformation, therefore, is a \(4 \times 4\) matrix because there are 4 elements in the vector. If \(L_{\alpha\beta}\) is a an arbitrary element of this matrix (row \(\alpha\) column \(\beta\), where the Greek letters stand for 0, 1, 2, and 3), the transformation matrix has the form:

(4.2)\[\begin{split}{\cal L}_{\alpha\beta} = \begin{bmatrix} L_{00} & L_{01} & L_{02} & L_{03}\\ L_{10} & L_{11} & L_{12} & L_{13}\\ L_{20} & L_{21} & L_{22} & L_{23}\\ L_{30} & L_{31} & L_{32} & L_{33} \end{bmatrix}\end{split}\]

The problem then is to figure out what the 16 numbers in \({\cal L}\) are that will achieve our goal. Note this is not quite the same thing as Einstein notation – in later chapters we’ll see how the sub and superscript notation works for the Lorentz matrix, but here I’m just using \(\alpha\) and \(\beta\) as ways of counting rows and columns.

Warning

Note that the \(\beta\) used as the index counter of the matrices has nothing to do with the relative velocity \(\beta_R\). Sometimes other Greek letters are used for counting indices, \(\mu\) and \(\nu\) in particular. You must notice how the letter is being used to be able to tell whether \(\beta\) is a speed or a matrix index.

4.2. Determining the Elements

Is there a way that we can determine some of the elements of the of the Lorentz transformation? We must figure out how the transformation works in specific cases, and these cases will then point to general values that could be used in any situation. All that we really know about the Lorentz transformation is that the 4-vector that is produced by its operation on the original 4-vector must have the same size as the first 4-vector, or the Michelson-Morley experimental results would be contradicted.

To determine some of the elements of the Lorentz transformation matrix, consider what happens when the displacement 4-vector

(4.3)\[\begin{split}[dx_4] = \begin{bmatrix} icdt\\ dx\\ dy\\ dz \end{bmatrix}\end{split}\]

is transformed from one inertial reference frame to another. If the relative velocity is in the \(x\)-direction, then displacements in the \(y\) and \(z\) directions won’t change. This derives from the independence of motion along perpendicular axes: if I am 10 m south of you, and I take one step East, I will still be 10 m South of you (assuming we are far from the poles, of course).

Note

Although the displacements perpendicular to the direction of relative motion are not affected by a Lorentz transformation, this independence does not apply to any object that you might perform a Lorentz transformation on. In electromagnetism, for example, the electric and mangetic fields in the \(y\) and \(z\) direction are different in a frame moving in the \(x\) direction. We use the dimensional independence of \(dy\) and \(dz\) to derive values for \({\cal L}\), but once we do that we don’t have to insist that the \(y\) and \(z\) for all vectors are unaffected in all circumstances at all times. Be cautious.

This means that \(dy^\prime = dy\). However, if we write out the third row of Equation (4.1), we get

\[dy^\prime = L_{20}icdt+L_{21}dx +L_{22}dy + L_{32}dz.\]

The only way this equality can hold for all displacement four vectors (which is to say for any values of \(dt\), \(dx\), \(dy\), and \(dz\)) is if \(L_{22}=1\) and the other elements are zero. The same logic can be applied to the fourth row to deduce \(L_{33}=1\), so we know the matrix must look like

(4.4)\[\begin{split}{\cal L} = \begin{bmatrix} L_{00} & L_{01} & L_{02} & L_{03}\\ L_{10} & L_{11} & L_{12} & L_{13}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

That takes care of half the numbers in one go!

To get the next set, we have to look at a particular case. Consider the examples at the end of Chapter 3. They all involved switching from a reference frame where two events were at rest into a reference frame in which there would have to be motion for something to get from one event to the other. We know therefore that the original four displacement is

(4.5)\[\begin{split}[dx_4] = \begin{bmatrix} icdt_0\\ 0\\ 0\\ 0 \end{bmatrix}\end{split}\]

We can also figure out what the transformed components have to be. We know that the time interval will be dilated in the primed frame: \(dt = \gamma_R dt_0\). Furthermore, if the events are at rest in the original frame, and the primed frame is moving to the right at speed \(\beta_R\), then from the point of view of the primed frame, the location of the events would have to be moving left at the same speed, so \(dx^\prime = -v_Rdt = -\beta_R cdt = -\beta_R\gamma_R cdt_0\), where we have used time dilation to turn the \(dt\) into \(dt_0\).

That gives us two further relations that will enable us to get four of the numbers. We look at the first two rows of Equation (4.1), using Equation (4.5) as the four vector:

\[icdt^\prime = L_{00}icdt_0\]

and

\[dx^\prime = L_{10}icdt_0.\]

The first of these two equations will get you back the time dilation if you take \(L_{00}=\gamma_R\), and then the second equation matches with the equation for \(dx^\prime\) as long as \(L_{10}=i\beta_R\gamma_R\).

This leaves us with (so far):

(4.6)\[\begin{split}{\cal L} = \begin{bmatrix} \gamma_R & L_{01} & L_{02} & L_{03}\\ i\beta_R\gamma_R & L_{11} & L_{12} & L_{13}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

The number of unknowns in the Lorentz transformation matrix has decreased from 16 to 6. The rest can be found using similar tricks. For example, you could set up the events in Fig. 4.1 such that the primed observer was in the rest frame of the events and work out the values for the rest of the unknowns. When all such tricks are exhausted, the Lorentz transformation between two frames of reference (Fig. 4.1) that have a relative speed of \(\beta_R\) in the positive x direction is given by the matrix:

(4.7)\[\begin{split}\boxed{ {\cal L}_x(\beta_R) = \begin{bmatrix} \gamma_R & -i\beta_R\gamma_R & 0 & 0\\ i\beta_R\gamma_R & \gamma_R & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} }\end{split}\]

The subscript \(x\) is to remind us that the relative velocity is in the \(x\) direction. If that were not the case, the matrix would look a lot more complicated! Note that this formulation is based on the diagram in Fig. 4.1 – if the velocity were in the opposite direction, the \(\beta_R\) would become \(-\beta_R\), the inverse Lorentz transformation.

4.3. Examples of Lorentz Transformations

4.3.1. Transform a Displacement Four-vector

An observer measures the 4-displacement between two events:

(4.8)\[\begin{split}[dR_4] = \begin{bmatrix} i3.00~{\rm m}\\ 1.00~{\rm m}\\ -0.250~{\rm m}\\ 0.00~{\rm m} \end{bmatrix}\end{split}\]

A second observer, traveling with speed \(1.31\times10^8\)~m/s in the \(x\) direction with respect to the first observer measures the 4-displacement for these same two events. What values of the elements of the 4-displaceinent does this second observer measure?

To solve this problem, you use the form of the Lorentz transformation in equation (4.7), plugging in the numbers. We know that \(\beta_R = v_R/c = 1.31/3.00 = 0.4367\), and therefore \(\gamma_R=1.1116\). Multiply the two to get \(\beta_R\gamma_R=0.4854\).

Now, we are ready to find the elements of \([dR_4]'\)

(4.9)\[\begin{split}[dR_4]' = {\cal L}_x(\beta_R)[dR_4] = \begin{bmatrix} 1.1116 & -i0.4854 & 0 & 0\\ i0.4854 & 1.1116 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} i3.00~{\rm m}\\ 1.00~{\rm m}\\ -0.250~{\rm m}\\ 0.00~{\rm m} \end{bmatrix}\end{split}\]

multiplying out the matrix gives

\[\begin{split}[dR_4]' = \begin{bmatrix} 1.1116(i3.00~{\rm m})-i0.4854(1.00~{\rm m})+0+0\\ -0.4854(3.00~{\rm m})+1.1116(1.00~{\rm m})+0+0\\ 0+0+-0.250~{\rm m}+0\\ 0+0+0+0.00~{\rm m} \end{bmatrix} = \begin{bmatrix} i2.8493~{\rm m}\\ -0.3446~{\rm m}\\ -0.2500~{\rm m}\\ 0.0000~{\rm m} \end{bmatrix}\end{split}\]

As a check, you can note that the size of the two four-vectors is the same:

\[[dR_4]^2 = (-3.00^2+1.00^2+(-0.250)^2+0.0^2)~{\rm m}^2 = -7.9375~{\rm m}^2\]

and

\[[dR_4]'^2 = (-2.85^2+(-0.34)^2+(-0.250)^2+0.00^2)~{\rm m}^2 = -7.9375~{\rm m}^2\]

Note which minus signs are squared (and therefore go away) and which ones are not. Also note that all components have units of length.

4.3.2. Graphical Lorentz Transform

Fig. 4.2 Interactive spacetime diagram. A displacement four vector is shown as a white arrow, the space component is green, and the time component is magenta. Moving the slider will transform this four vector into a reference frame moving at a relative speed shown to the right of the slider.

It is possible, even easy, to program a computer to perform a Lorentz transformation on any four-vector you might like to contemplate from another inertial reference frame. Fig. 4.2 illustrates this process. A displacement vector

(4.10)\[\begin{split}[dR_4] = \begin{bmatrix} i0.6~{\rm m}\\ 0.3~{\rm m}\\ \end{bmatrix}\end{split}\]

is shown as a white arrow when \(\beta_R=0.0\). There is a red sphere at \([dR_4]_{red} = [i0.1~{\rm m},0.3~{\rm m}]\) and a blue sphere at \([dR_4]_{blue} = [i0.4~{\rm m},0.9~{\rm m}]\). The displacement four-vector shows the displacement from red to blue. If you move the slider to a different \(\beta_R\), the computer will Lorentz Transform the four-position of each sphere and then recalculate the four-displacement between the red and blue events. You should verify yourself in a few cases that the numbers are being calculated correctly.

Note

Programming a Lorentz Transformation

It would be a very good idea for you to write your own code that takes a \(\beta_R\) and a four vector and returns the transformed four vector. You could also write it to return the size of the four vector before and after the transformation, so you could verify that it hasn’t changed. You could write the code to set up and multiply matrices, or you could write the four equations out separately. Which method you use would be irrelevant to the output.

4.3.3. Angles in Space

Find the physical angle that the displacement given in Example 4.3.1 makes with respect to the \(x\) axis. Determine the angle as measured by the primed observer.

In Example 4.3.1, there is a displacement four-vector with \(dx=1.00\) m and \(dy=-0.250\) m. Trigonometry tells us that the tangent of the angle with the \(x\) axis is the height over the base, \(dy/dx\). Therefore, the angle that the unprimed observer makes is:

\[\tan{\theta} =\frac{dy}{dx} = \frac{-0.250~{\rm m}}{1.00~{\rm m}} = -0.25 \rightarrow \theta = -14.0^\circ\]

The angle is in the 4th quadrant.
This makes sense since \(dy\) is negative and \(dx\) is positive.

The second observer moving with respect to the first measures an angle:

\[\tan{\theta^\prime} =\frac{dy'}{dx'} = \frac{-0.250~{\rm m}}{-0.351~{\rm m}} = 0.712 \rightarrow \theta^\prime = 234.0^\circ\]

This angle is in the third quadrant as both \(dx'\) and \(dy'\) are negative. Essentially, the second observer is overtaking the first, so the horizontal displacement flips around and points the other way.

4.3.4. Using an Inverse Lorentz Transformation

The primed observer in example 4.3.1 believes that the unprimed observer is moving with speed \(v_R = 1.3\times10^8\) m/s in the \(-x\) direction with respect to him. Show that this is a reasonable assumption by finding the elements of the inverse Lorentz transformation that transform the coinponents she measured for \([dR4]'\) into those measured by the observer in the unprimed reference frame. In other words, imagine you didn’t know \(\beta_R\) and find it from the given four vectors.

Going back to the transformation in example 4.3.1, but setting it up as an inverse transformation, we get:

(4.11)\[[dx_4] = {\cal L}_x(-\beta_R)[dx_4]'\]

\[\begin{split}\begin{bmatrix} i3.00~{\rm m}\\ 1.00~{\rm m}\\ -0.250~{\rm m}\\ 0.00~{\rm m} \end{bmatrix} = \begin{bmatrix} \gamma_R & i\beta_R\gamma_R & 0 & 0\\ -i\beta_R\gamma_R & \gamma_R & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} i2.79~{\rm m}\\ -0.351~{\rm m}\\ -0.250~{\rm m}\\ 0.00~{\rm m} \end{bmatrix}\end{split}\]

Note the minus sign has been switched. The \(y\) and \(z\) components don’t change, but if you work out the first two components and then take their ratio, you get

\[\frac{dx}{cdt}=\frac{1.00~{\rm m}}{3.00~{\rm m}} = \frac{\gamma_R[-0.351~{\rm m} + \beta_R(2.79~{\rm m})]}{\gamma_R [2.79~{\rm m}-\beta_R(0.351~{\rm m})]}\]

The factors of \(\gamma_R\) cancel, and then you can sove for \(\beta_R\) to get \(\beta_R = 0.44\) which means \(v_R = 1.3\times10^8\) m/s, as expected.

4.4. Problems

1. A star is \(25.0\) light years away from the earth. If a space craft were to travel with \(\beta = 0.998\) with respect to the earth, how long would it take the space craft to reach the star as measured by an observer on the Earth? Set up a displacement four vector and use the Lorentz Transformation to find the time as measured by an observer aboard the space craft.

2. In this problem, you will find two more elements of the Lorentz transformation matrix. In Equation (4.6), there are still 6 unknown elements. To get two more, consider this setup: the primed observer finds that she is in the rest frame of a pair of events. She measures a time interval \(dt_0\) between the events. A second observer, moving with speed \(-\beta_R\) with respect to the primed observer watches the same two events and measures a physical displacement \(dx\) and a time interval \(dt\).

a) write down the elements of the Lorentz transformation that converts the values measured by the primed observer and to those measured by the unprimed observer using the form of the Lorentz transformation given by Equation (4.6).

b) Multiply out the elements of this matrix equation and show how \(dt_0\) (time measured in the rest frame of the events) is related to \(dx\) and \(dt\).

c) knowing that the size of the two 4-vectors must be the same, find values for \(L_{11}\) and \(L_{01}\).

3. An arbitrary 4-vector \(v^\alpha\) has components: \(v^0\), \(v^1\), \(v^2\), and \(v^3\).

a) Write this 4-vector in column vector notation.

b) If this 4-vector is operated on by a Lorentz transformation of relative speed \(\beta_R\) in the \(+x\) direction, find the components of the new 4-vector using Equations (4.1) and (4.7).

c) Show that the size of the two 4-vectors are the same.

4. An observer in the rest frame of two events measures a time interval of \(1.00~\mu\)s. A second observer, watching the same two events measures a time interval of \(1.50~\mu\)s.

a) what is the relative speed of the two observers?

b) write down the elements of the Lorentz transformation that transforms the components of the 4-vectors between these two observers.

c) How for did the second observer see the events displace?

5. A scalar quantity in relativity is one whose value does not change when Lorentz Transformation Introduction to Special Relativity the Lorentz transformation is applied to it.

6. Show that the size of the displacement 4-vector is a scalar quantity.

b) Show that the time interval measured in the rest frame of two events, \(dt_0\), is a scalar quantity.

7. Two observers are watching two events taking place are traveling at relative speed \(\beta_R = 0.9950\). The first observer manages to measure a time interval of \(6.00\) ns, but does not measure the displacement \(dx\). The second observer manages to measure a displacement of \(4.00\) m in the \(-x\) direction between the two events. Find the value of the displacement \(dx\) that the first observer did not measure.

8. The ‘unit matrix’ or ‘identity matrix’ has the number 1 along the diagonal elements and has value of \(0\) for all of the off diagonal elements. In general, if a matrix has an inverse, then:

(4.12)\[M^{-1} M = {\rm unit~matrix}\]

Show that for the Lorentz transformation matrix

(4.13)\[\begin{split}{\cal L}_x^{-1}(\beta_R){\cal L}_x(\beta_R) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

9. When a new theory is proposed, in the region where the old theory worked, the new theory must reduce to the same form as the old. This requirement for new theories is called the correspondence principle, first articulated by Niels Bohr. The Lorentz transformation is supposed to work for all relative motion problems, whether the relative speed is large or small. For slow moving objects, Newton found that the time measured by all observers is the same.

\[dt' = dt\]

He also found that if two observers moving at a speed \(v_R\) with respect to each other watch an object move, the two measured displacements are reiated as:

\[dx'= dx- v_Rdt\]

provided the relative speed of the primed observer in the same direction as the object moves.

Show that if \(\beta_R\ll 1\) (slow moving), the Lorentz transformation equation for the displacement 4-vectors as written in (4.1) and (4.7) gives the same predictions as Newton found for slow moving objects.

Hint: To do this you first must rewrite the Lorentz transformation matrix for very very small \(\beta_R\). Then find the values of \(dx'\) and \(dt'\) in terms the unprimed values of \(dx\) and \(dt\). Again, making sure that \(\beta_R\) is very small compared to 1, show that Newton’s and Lorentz’s predictions are not different.